The class of grammar-based fractals known as Lindenmayer system allows generating an interesting variety of geometrical and botanical visuals.

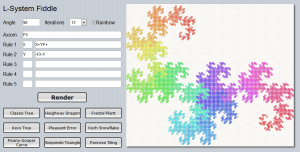
To the right is a representation of a “Fractal Plant”, which is generated from just two simple (if cryptic-looking) rules applied recursively.

In simple terms, L-System starts from a string (called an axiom), to which rules are applied recursively. Rules are a set of substitution strings for characters in the original string.

Classic Algae

For illustration,the classic example (named “Algae”), has two rules:

A -> AB  (each A becomes AB)
B -> A (each B becomes A)

And when you start from “A” as axiom, that gives the following recursive sequence:

n = 0 : A
n = 1 : AB
n = 2 : ABA
n = 3 : ABAAB
n = 4 : ABAABABA

Obtaining graphics

When you couple the above system with Turtle graphics, these strings can be used as the basis of a vector drawing. Combine a well chosen grammar with a bit of coloring, and you can obtain visually pleasing fractals.

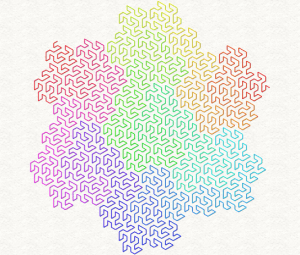Lindenmayer started from a botanical perspective, but the grammar system can be applied to a variety of mathematical entities, like the Peano-Gosper curve you can see to the left.

A variety of tilings and Kolams can also be achieved.

Coloring can be handled via turtle language commands directly, but also by coloring the lines from start to finish, such as in the Peano-Gosper curve here, where the colors are taken form a rainbow 1D texture.

Finally, L-System fractals also are an interesting way to stress-test a graphics UI line-rendering capabilities 😉

Start Fiddling Now!

I’ve made a small SmartMS app where you can fiddle with L-System right from any browser (desktop or mobile), along with a few classic presets to get you started:

L-System Fiddle

For the curious ones, timings are listed in the JavaScript console, f.i. hit ctrl+shift+J in Chrome to bring it up.

Now let’s get under the hood!

Applying L-System grammar

Below is the source code for applying a set of grammar rules to an axiom. They’re implemented as a simple set of  helper methods to an array of L-System rules.

Let’s suppose you want to generate the Heighway Dragon up to iteration 12, that can be done with just

var rules : TLSystemRules;
rules.Add('X', 'X+YF+');
rules.Add('X', '-FX-Y');
var dragon := rules.Apply('FX', 12);

As you see the helper approach allows to keep the code very simple. As to what can be done with the “dragon” string that’ll be topic for part 2 😉

I’ll leave you with the unit that allows the above code to work it magic.

unit LSystem;

interface

type

   TLSystemRule = record
      Predecessor : String;
      Successor : String;
   end;

   TLSystemRules = array of TLSystemRule;

   TLSystemRulesHelper = helper for TLSystemRules
      procedure AddRule(const predecessor, successor : String);

      function Apply(const axiom : String) : String; overload;
      function Apply(const axiom : String; iterations : Integer) : String; overload;
   end;

implementation

{ TLSystemRulesHelper }

procedure TLSystemRulesHelper.AddRule(const predecessor, successor : String);
var
   r : TLSystemRule;
begin
   r.Predecessor := predecessor;
   r.Successor := successor;
   Self.Add(r);
end;

function TLSystemRulesHelper.Apply(const axiom : String) : String;
var
   i : Integer;
   s : String;
   rule : TLSystemRule;
begin
   for i := Low(axiom) to High(axiom) do begin
      s := axiom[i];
      for rule in Self do begin
         if s = rule.Predecessor then begin
            s := rule.Successor;
            break;
         end;
      end;
      Result += s;
   end;
end;

function TLSystemRulesHelper.Apply(const axiom : String; iterations : Integer) : String;
begin
   Result := axiom;
   while iterations > 0 do begin
      Result := Apply(Result);
      Dec(iterations);
   end;
end;