Fiddling with L-System (part 1)

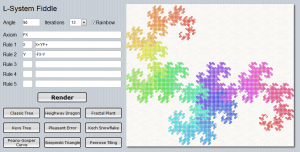
^[1]The class of grammar-based fractals known as Lindenmayer system ^[2] allows generating an interesting variety of geometrical and botanical visuals.

To the right is a representation of a “Fractal Plant”, which is generated from just two simple (if cryptic-looking) rules applied recursively.

In simple terms, L-System starts from a string (called an axiom), to which rules are applied recursively. Rules are a set of substitution strings for characters in the original string.

Classic Algae

For illustration,the classic example (named “Algae”), has two rules:

A -> AB  (each A becomes AB)
B -> A (each B becomes A)

And when you start from “A” as axiom, that gives the following recursive sequence:

n = 0 : A
n = 1 : AB
n = 2 : ABA
n = 3 : ABAAB
n = 4 : ABAABABA

Obtaining graphics

When you couple the above system with Turtle graphics ^[3], these strings can be used as the basis of a vector drawing. Combine a well chosen grammar with a bit of coloring, and you can obtain visually pleasing fractals.

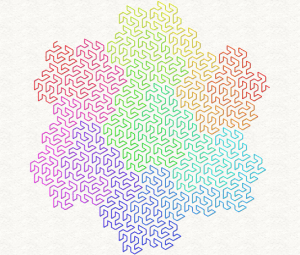^[4]Lindenmayer ^[5] started from a botanical perspective, but the grammar system can be applied to a variety of mathematical entities, like the Peano-Gosper curve you can see to the left.

A variety of tilings and Kolams ^[6] can also be achieved.

Coloring can be handled via turtle language commands directly, but also by coloring the lines from start to finish, such as in the Peano-Gosper curve here, where the colors are taken form a rainbow 1D texture.

 

Finally, L-System fractals also are an interesting way to stress-test a graphics UI line-rendering capabilities 😉

Start Fiddling Now!

I’ve made a small SmartMS ^[7] app where you can fiddle with L-System right from any browser (desktop or mobile), along with a few classic presets to get you started:

For the curious ones, timings are listed in the JavaScript console, f.i. hit ctrl+shift+J in Chrome to bring it up.

Now let’s get under the hood!

Applying L-System grammar

Below is the source code for applying a set of grammar rules to an axiom. They’re implemented as a simple set of  helper methods to an array of L-System rules.

Let’s suppose you want to generate the Heighway Dragon ^[9] up to iteration 12, that can be done with just

var rules : TLSystemRules;
rules.Add('X', 'X+YF+');
rules.Add('X', '-FX-Y');
var dragon := rules.Apply('FX', 12);

As you see the helper approach allows to keep the code very simple. As to what can be done with the “dragon” string that’ll be topic for part 2 😉

I’ll leave you with the unit that allows the above code to work it magic.

unit LSystem;

interface

type

   TLSystemRule = record
      Predecessor : String;
      Successor : String;
   end;

   TLSystemRules = array of TLSystemRule;

   TLSystemRulesHelper = helper for TLSystemRules
      procedure AddRule(const predecessor, successor : String);

      function Apply(const axiom : String) : String; overload;
      function Apply(const axiom : String; iterations : Integer) : String; overload;
   end;

implementation

{ TLSystemRulesHelper }

procedure TLSystemRulesHelper.AddRule(const predecessor, successor : String);
var
   r : TLSystemRule;
begin
   r.Predecessor := predecessor;
   r.Successor := successor;
   Self.Add(r);
end;

function TLSystemRulesHelper.Apply(const axiom : String) : String;
var
   i : Integer;
   s : String;
   rule : TLSystemRule;
begin
   for i := Low(axiom) to High(axiom) do begin
      s := axiom[i];
      for rule in Self do begin
         if s = rule.Predecessor then begin
            s := rule.Successor;
            break;
         end;
      end;
      Result += s;
   end;
end;

function TLSystemRulesHelper.Apply(const axiom : String; iterations : Integer) : String;
begin
   Result := axiom;
   while iterations > 0 do begin
      Result := Apply(Result);
      Dec(iterations);
   end;
end;