After looking at String concatenation and String Building in Delphi, and as a conclusion, it’s time to have a brief look at what happens in multi-threaded settings, such as in a server pushing JSON, XML or some other text data.
Benchmark Results
The test case is the same as that of the String Building article, except from a multi-threaded environment.
The following graphs plots the time it takes for 1 to 8 threads to go through a given workload (100 times the 10k case), on a quad-core CPU. Lower values are better
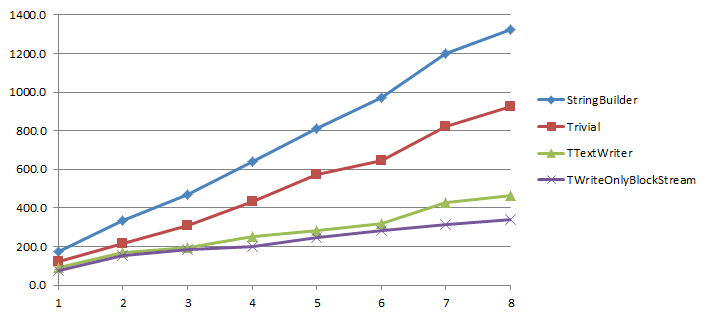
As a reminder of the participants:
- StringBuilder is the RTL’s TStringBuilder class
- Trivial is using plain String concatenation with the “:=” and “+” operators
- TTextWriter is the mORMot/Synopse class (it’s the only one operating in utf-8)
- TWriteOnlyBlockStream is the DWScript class from dwsUtils
TStringStream is just off-the-chart, literally-speaking, it’s already beyond 2200 in the 4 threads case.
In terms of CPU usage:
- StringBuilder and Trivial cases only use one CPU, their bottlenecks are the RTL functions for String reference counting and the memory manager (Delphi-side).
- TTextWriter and TWriteOnlyBlockStream bottlenecks are found in the concatenations, integer-to-string conversions, and VirtualAlloc calls to Windows.
Interestingly enough, for both mORMot and DWScript test, the main VCL thread remained smooth and responsive during the tests, while with TStringBuilder, it was not, despite a lower overall CPU usage.
Follow this link for the source code.
Previous articles:
The memory-manager is the main culprit here.
I noticed in Delphi XE2 (I don’t use any of the later versions), that using FASTMM4 and enabling NeverSleepOnThreadContention in FastMM4Options.inc *greatly* increases performance for multi-threaded string-handling.
The problem is that per default the memory-manager will yield the current thread if it cannot access one of its internal data-structures because another thread is accessing those at the same time. That means the current thread will sleep until it gets re-awakened by the operating-system. And that can easily take about 20ms. In a heavily multi-threaded environment this can almost make your multi-threaded application look like it’s single-threaded. 🙂
I don’t know if later Delphi versions still behave in the same way. But it’s worth a try I think.
NeverSleepOnThreadContention will only work in very particular workloads, that’s why it’s off by default.
In practice you should only use NeverSleepOnThreadContention when the number of threads is below the numbers of cores (real cores, not hyper-threaded ones), and you’re sure you don’t have any thread doing tight accesses, otherwise it’ll just keep the CPU very busy and make everything far worse.
See for instance: http://www.thedelphigeek.com/2011/09/neversleeponthreadcontentionnot.html
It may be interesting to run the test with SynScaleMM or even better ScaleMM2 instead of FastMM4.
TTextWriter and TWriteOnlyBlockStream are about 3 times faster than StringBuilder.
What could be interesting may be to benchmark typical JSON creation, e.g. an array of objects.
@A.Bouchez The speed difference goes up to 3.9 actually for WOBS. ScaleMM2 may matter for StringBuilder, but I’m not sure it would help TextWriter or WOBS, unless it retains a lot more memory from the OS to cut down on the VirtualAlloc calls.
The benchmark is actually close to a typical JSON creation, as it alternates constant and dynamic strings. However a JSON would probably see more short strings (commas, quotes, etc.), which would make StringBuilder look worse as it relies on System.Move even for very short strings.
I have an HTML-parser that uses 10 threads on a 4-core machine (plus hyper-threading). With NeverSleepOnThreadContention enabled, it is way, WAY faster. That parser is processing about 1000 HTML-pages per second. So there is a LOT of string-handling goint on. Lots of memory-allocations and releases.
These benchmarks are great. Thanks.
Would you consider sharing your source code so other people can replicates your results and try to fine tune the performance? Maybe even try them against different versions of Delphi.
I replicated some of your previous testing with your help, but using a working example as a starting point will save some back and forth and people using slightly different assumptions.