 When looking up a string, what is the fastest strategy?
When looking up a string, what is the fastest strategy?
A hash map, a sorted list or an unsorted list?
Of course it depends on how many strings you have, but where are the cutoff points?
Here is a quick test, and an interesting tidbit is uncovered…
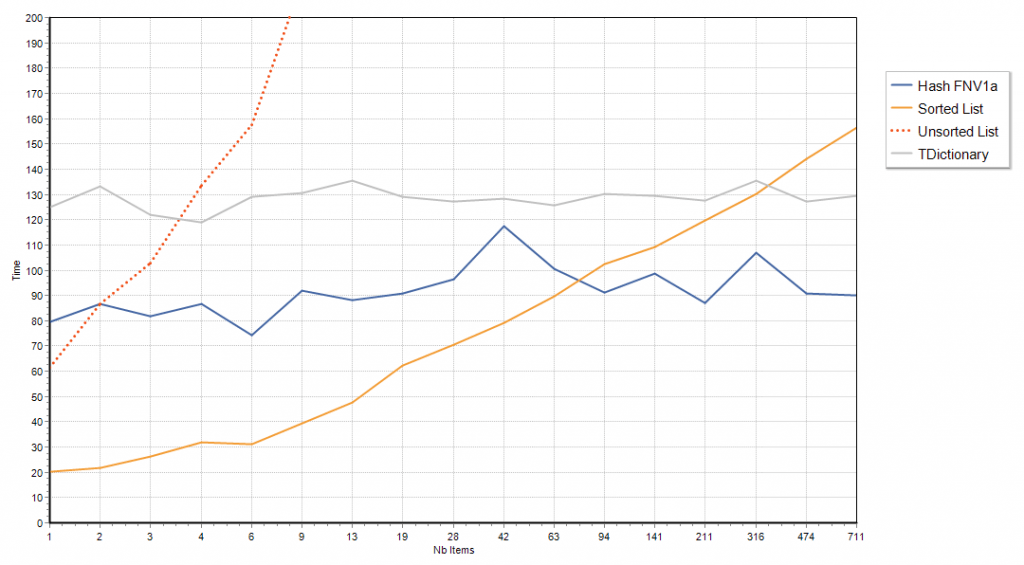
Without further ado, here is the result chart.
Time is the vertical axis (lower is better), horizontally is the number of items, note that it is logarithmic.
Those are results for random, 12 characters strings, but the curves where almost unchanged if the strings were “less random” (with 6 identical characters at the start f.i.)
“TDictionary” and “Hash FNV1a” are both hash-maps, but “Hash FNV1a” uses a fast hash, while “TDictionary” uses the slower Bob-Jenkins Hash (which is also more prone to collisions, but these did not affect that particular test)
Observations
- avoid using an unsorted list 🙂
- if you have a few dozen strings, a simple sorted list can be preferable
- computing a hash code is hardly innocuous, with a slow hash you need to have hundreds of items just to get even on hash-code computations
Tidbit of note
Sorted & Unsorted lists are both using TStringList, with just an overloaded CompareStrings method hardcoded to a case-insensitive comparison, and the difference is just whether Sorted is set to true or not… so why the difference even for the case where you have 1 or 2 elements?
In both cases IndexOf() was called, but IndexOf merely reroutes the execution to TStrings.IndexOf or TStringList.Find depending on the value of Sorted, and that makes all the difference…
- TStringList.Find accesses the FList private field directly, and so involves no reference counting, and no exception frames.
- TStrings.IndexOf on the other hand goes through the Get method, which means a reference count and an implicit exception frame, which when you’re comparing a single string or two bites a lot.
When there are a couple elements, an unsorted search in TStringList is actually spent doing a fair share of Automatic Reference Counting tasks (there is also a bit of range checking, but it’s negligible in comparison).



I would like very much if you post the source code. I wish to test with very long strings, like SQL queries…
The search on a sorted list should not grow “Linearly” if you are doing Binary search… Does Find or IndexOf uses Binary search?
That number of items is the actual value of it is “Thousands”?
Can you show us the source code of the test?
I wonder if a dictionary can be optimized even further by storing the hashed integers into a sorted list and doing the binary search (Find) against it? As long as the collision count was small, I would expect the results to be better than the sorted string list results. Of course the trade off would be memory and the time it takes to sort.
Thank you, good job
@Matheus @Blikblum It’s quite simple really https://dl.dropboxusercontent.com/u/25996884/Unit89.zip
@Matheus just did a quick test with 250-character ling strings, where the first 128 chars are the same and the rest random (so as not to give the sorted string list too much of an advantage), well, the sorted list just dominates… http://i.imgur.com/AtsCVFJ.png and none of the hashes can pay for themselves up to a few hundred strings…
@Eric The sorted list does a binary search, but the horizontal axis is asymptotically logarithmic hence the linearity (asymptotically as the values have to be integers though, so this skews the first few values). The number of items is the actual number of items.
@Steven There is not problem in the dictionary with finding the string once you have its hash, the problem is computing the hash in the first place. This has a fixed, non-negligible cost, which grows with the string length.
So seems the conclusion is that if you are using short strings and looking for them:
1) NEVER unsorted;
2) Sorted until ~80 itens;
3) Hash FNV1a any other case;